Polynomial Evaluation by Divide and Conquer
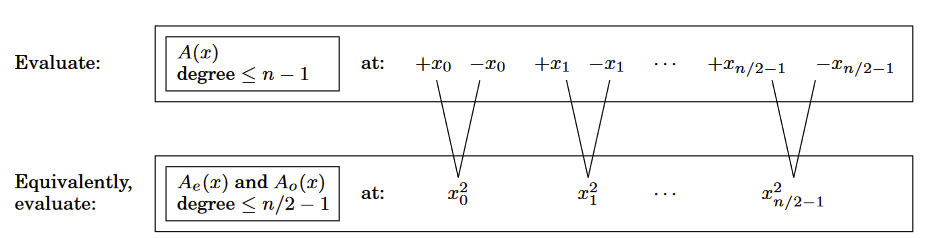
We have to pick points to evaluate a polynomial with degree , we can pick positive negative pairs
Then the computations required for each and overlap a lot, because the even powers of coincide with those of .
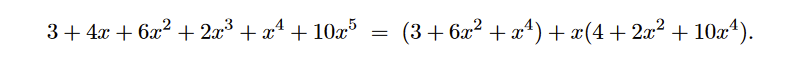
To generalize, write
Runtime analysis:
We use complex numbers!
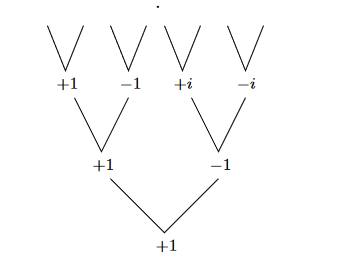
By reverse-engineering from the bottom, we eventually reach the initial set of points. Perhaps you have already guessed what they are: the complex nth roots of unity, that is, the complex solutions to the equation .
Figure 2.6 is a pictorial review of some basic facts about complex numbers. The third panel of this figure introduces the nth roots of unity: the complex numbers $$1, \omega, \omega^2, \dots , , where . If is even,
1. The nth roots are plus-minus paired,
2. Squaring them produces the -nd roots of unity.
Therefore, if we start with these numbers for some n that is a power of 2, then at successive levels of recursion we will have the -th roots of unity, for All these sets of numbers are plus-minus paired, and so our divide-and-conquer, as shown in the last panel, works perfectly. The resulting algorithm is the fast Fourier transform.
