Reduction: ZOE → RUDRATA CYCLE

Two steps:

1. Prove that ZOE can be reduced to a generalization of RUDRATA CYCLE, called RUDRATA CYCLE WITH PAIRED EDGES

2. How to get rid of the extra features of the problem and reduce it to the plain RUDRATA CYCLE

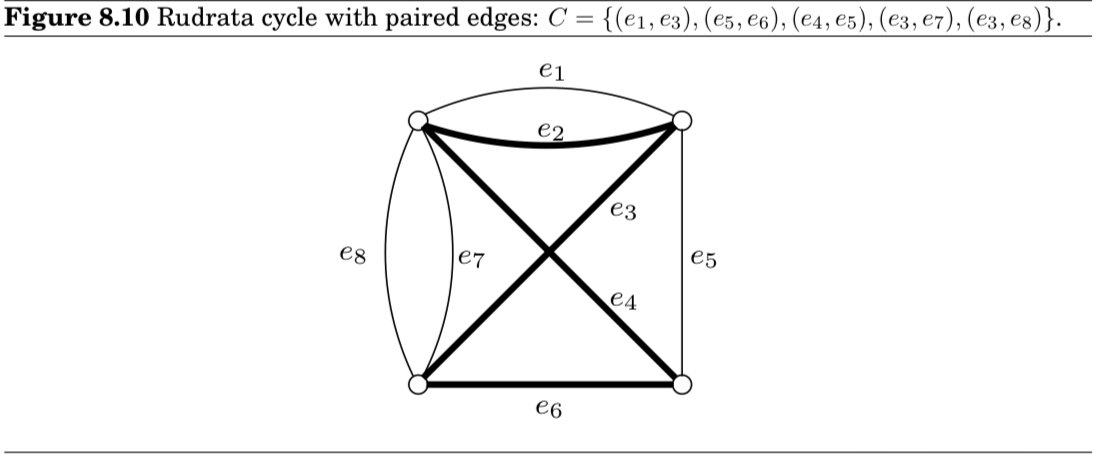
RUDRATA CYCLE with paired edges

Given a graph $G = (V,E)$ and a set $C \sube E \times E$ of pairs of edges. We seek a cycle that

1. visits all vertices once

2. For every pair of edges $(e, e’)$ in $C$, traverses exactly one of either $e$ or $e’$.

Reduction: ZOE ⇒ RUDRATA CYCLE WITH PAIRED EDGES

Given an instance of ZOE, $A\vec{x} = \vec{1}$ (A is $m \times n$ matrix with only 0-1 entries), the graph we can construct is:

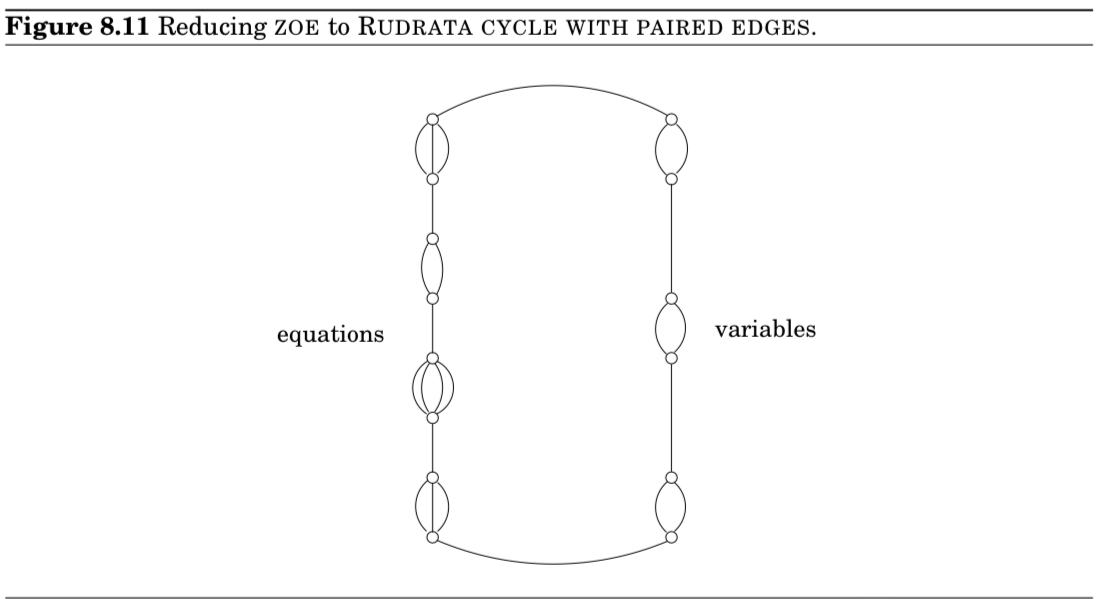
It’s a cycle that connects $m+n$ collections of parallel edges!

For each variable $x_i$ we have two parallel edges corresponding to $x_i = 1, x_i = 0$.

For each equation $x_{j1}+\cdots + x_{jk} = 1$ involving $k$ variables, we have $k$ parallel edges, one for every variable in the equation.

Therefore

• Any RUDRATA CYCLE in this graph must traverse the $m+n$ collections of parallel edges one by one, choosing one dge from each collection.

• The cycle “chooses” for each variable a value

However, the structure of matrix $A$ must be reflected somewhere ⇒ and that is the set $C$ of pairs of edges such that exactly one edge in each pair is traversed.

• For every equation, and for every variable $x_i$ in it,
  • Add to $C$ the pair $(e, e’)$ where $e$ is the edge corresponding to the appearance of $x_i$ in the equation (on the left side of the figure), and $e’$ is the edge corresponding to the variable assignment $x_i = 0$ (on the right side of the figure)

The construction is now complete, we claim the values chosen are a solution to the original instance of ZOE

• If a variable $x_i$ has value 1, then edge $x_i = 0$ is not traversed, and all edges associated with $x_i$ on the equation side must be traversed.

• Therefore each equation exactly one of the variables appearing in it has value $1$ - all equations are satisfied

Getting rid of edge pairs

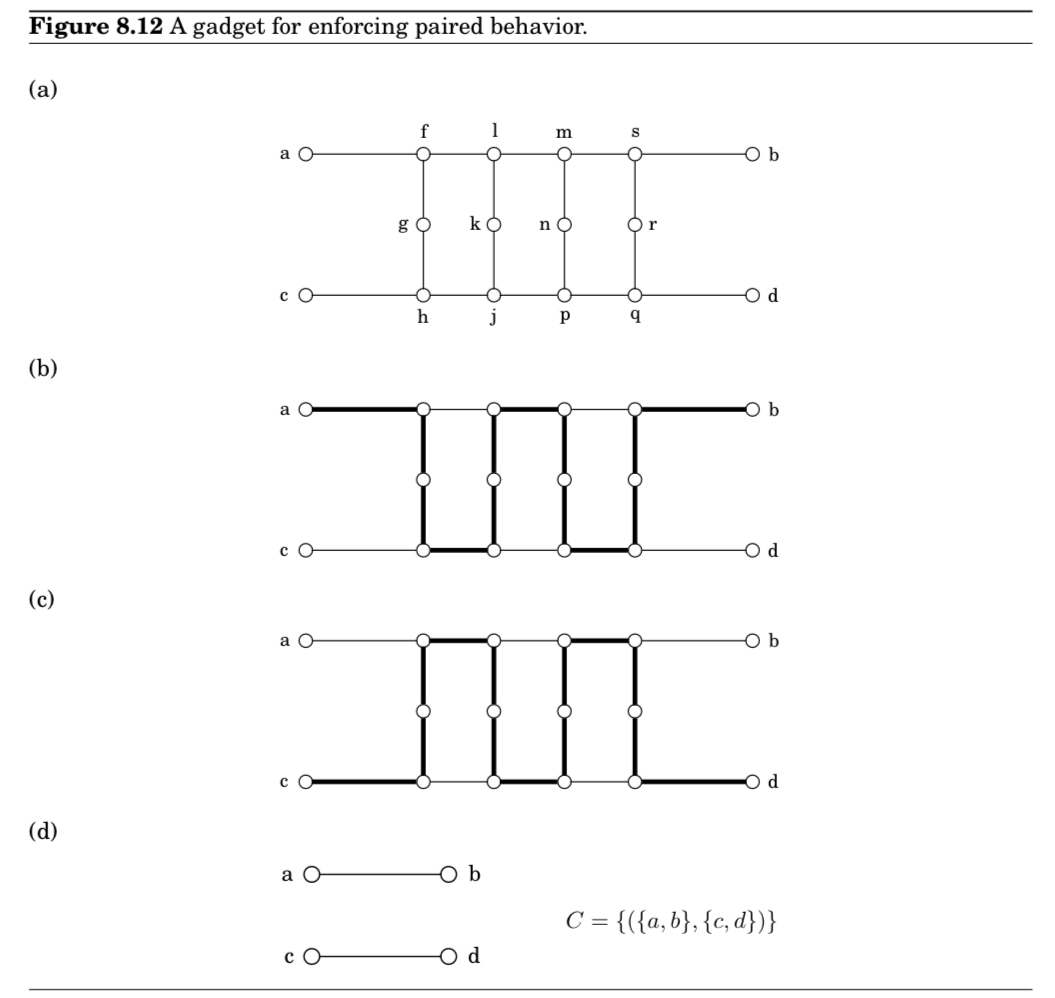
Suppose Figure 8.12 a) is a part of a larger graph $G$ in such a way that only the four endpoints $a,b,c,d$ touch the rest of the graph. We claim that this graph has the important property:

• In any Rudrata cycle of $G$ the subgraph shown must be traversed in one of the two ways shown in bold in Figure 8.12(b) and (c)
  • Suppose that the cycle first enters the subgraph from vertex $a$ continuing to $f$, then it must continue to vertex $g$ (because $g$ has degree 2 and it must be visited immediately after one of its adjacent nodes is visited).
  • Hence we must go on to node $h$ and here we seem to have a choice
    • continue to $j$
    • return to $c$
      • How are we going to visit the rest of the subgraph?
  • Go on and on…

• Basically: This gadget behaves just like the two edges $\{a,b\}, \{c,d\}$

To reduce RUDRATA CYCLE WITH PAIRED EDGES to RUDRATA CYCLE,

• we go through the pairs in $C$ one by one.

• For each pair $(\{a,b\}, \{c,d\})$, replace the two edges with the gadget in Fig 8.12(a)

• For any other pair in $C$ that insolves $\{a, b\}$, we replace the edge $\{a,b\}$ with the new edge $\{a, f\}$, where $f$ is from the gadget
  • Because the traversal of $\{a, f\}$ indicates that whether in the old graph $\{a,b\}$ would be traversed.

• Similarly, for any other pair in $C$ that involves $\{c,d\}$, replace with $\{c,h\}$.

• After $|C|$ such replacements (each performed in polynomial time), we are done!