To understand what duality is about, recall our introductory LP with the two types of chocolate:
max x 1 + 6 x 2 x 1 ≤ 200 x 2 ≤ 300 x 1 + x 2 ≤ 400 x 1 , x 2 ≥ 0 \max x_1 + 6x_2 \\
\begin{split}
x_1 &\le 200 \\
x_2 &\le 300 \\
x_1 + x_2 &\le 400 \\
x_1, x_2 &\ge 0
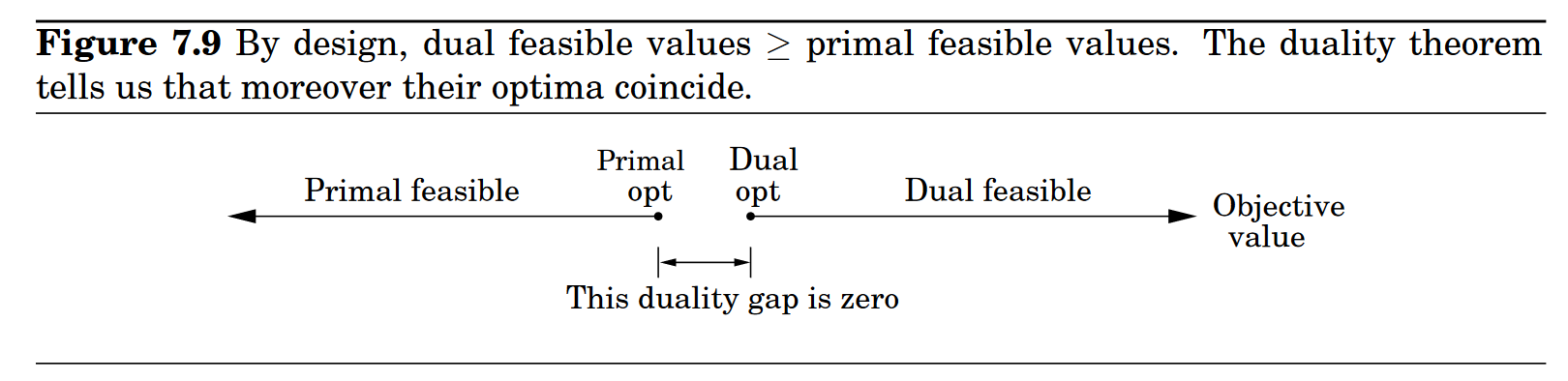
\end{split} max x 1 + 6 x 2 x 1 x 2 x 1 + x 2 x 1 , x 2 ≤ 200 ≤ 300 ≤ 400 ≥ 0 The simplex algorithm declares the optimum solution as ( x 1 , x 2 ) = ( 100 , 300 ) (x_1, x_2) = (100,300) ( x 1 , x 2 ) = ( 100 , 300 ) 1900 1900 1900
Suppose we multiply the tree equalities by 0 , 5 , 1 0,5,1 0 , 5 , 1
x 1 + 6 x 2 ≤ 1900 x_1 + 6x_2 \le 1900 x 1 + 6 x 2 ≤ 1900 The multiplirs ( 0 , 5 , 1 ) (0,5,1) ( 0 , 5 , 1 )
❓
But how do we systematically find it?
With the incentive above, we formulate our multipliers and call them y i y_i y i
Multiplier Inequality y 1 y_1 y 1 x 1 ≤ 200 x_1 \le 200 x 1 ≤ 200 y 2 y_2 y 2 x 2 ≤ 300 x_2 \le 300 x 2 ≤ 300 y 3 y_3 y 3 x 1 + x 2 ≤ 400 x_1 + x_2 \le 400 x 1 + x 2 ≤ 400
To start with, those y i y_i y i
( y 1 + y 3 ) x 1 + ( y 2 + y 3 ) x 2 ≤ 200 y 1 + 300 y 2 + 400 y 3 (y_1 + y_3)x_1 + (y_2+y_3)x_2 \le 200y_1+300y_2+400y_3 ( y 1 + y 3 ) x 1 + ( y 2 + y 3 ) x 2 ≤ 200 y 1 + 300 y 2 + 400 y 3 We want the left hand side to look like our objective function x 1 + 6 x 2 x_1 + 6x_2 x 1 + 6 x 2
x 1 + 6 x 2 ≤ 200 y 1 + 300 y 2 + 400 y 3 if { ∀ i , y i ≥ 0 y 1 + y 3 ≥ 1 y 2 + y 3 ≥ 6 x_1 + 6x_2 \le 200y_1 + 300 y_2 + 400y_3 \text{ if } \begin{cases}
\forall i, y_i \ge 0 \\
y_1 + y_3 \ge 1 \\
y_2 + y_3 \ge 6
\end{cases} x 1 + 6 x 2 ≤ 200 y 1 + 300 y 2 + 400 y 3 if ⎩ ⎨ ⎧ ∀ i , y i ≥ 0 y 1 + y 3 ≥ 1 y 2 + y 3 ≥ 6 Although we can let y i y_i y i want this bound to be a tight bound so should minimize 200 y 1 + 300 y 2 + 400 y 3 200y_1 + 300y_2 + 400y_3 200 y 1 + 300 y 2 + 400 y 3
Therefore now we have a new LP:
min 200 y 1 + 300 y 2 + 400 y 3 y 1 + y 3 ≥ 1 y 2 + y 3 ≥ 6 y 1 , y 2 , y 3 ≥ 0 \min 200y_1 + 300y_2 + 400y_3 \\
\begin{split}
y_1 + y_3 &\ge 1 \\
y_2 + y_3 &\ge 6 \\
y_1, y_2, y_3 &\ge 0
\end{split} min 200 y 1 + 300 y 2 + 400 y 3 y 1 + y 3 y 2 + y 3 y 1 , y 2 , y 3 ≥ 1 ≥ 6 ≥ 0 any feasible value of this dual LP is an upper bound on the original primal LP. So if we somehow find a pair of primal and dual feasible values that are equal, then they must be optimal.