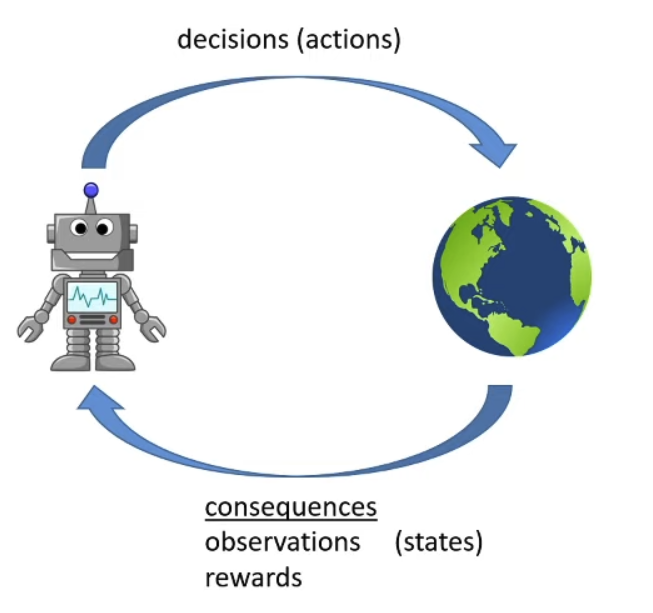
CS 285 Notes
Created by Yunhao Cao (Github@ToiletCommander) in Fall 2022 for UC Berkeley CS 285 (Sergey Levine).
Reference Notice: Material highly and mostly derived from Prof Levine's lecture slides, some ideas were borrowed from wikipedia & CS189.
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License
General Introduction to RL (LEC 1)

Compared to traditional reinforcement learning,
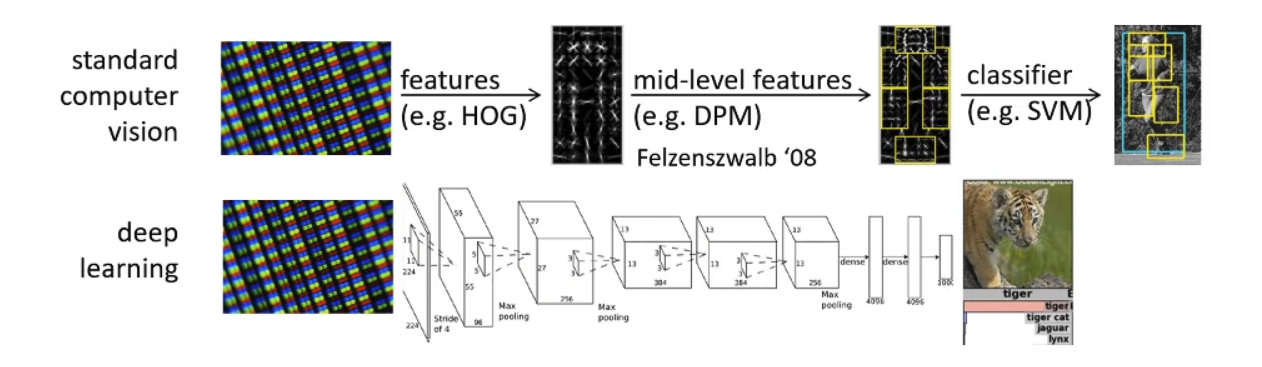
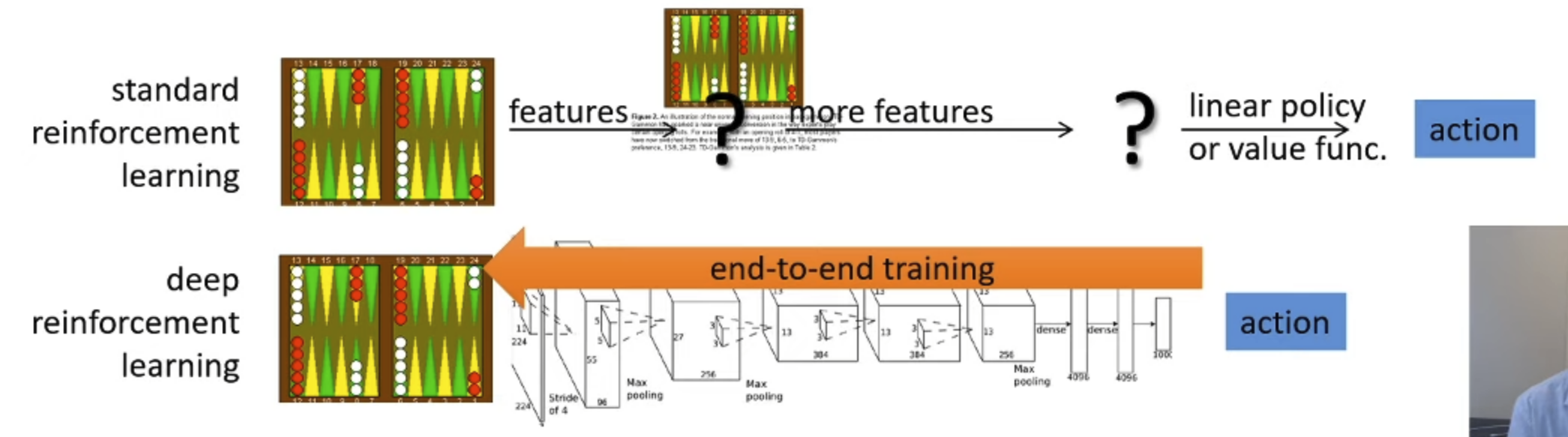
With DRL(Deep Reinforcement Learning), we can solve complex problems end-to-end!
But there are challenges:
- Humans can learn incredibly quickly
- Deep RLs are usually slow
- probably because humans can reuse past knowledge
- Not clear what the reward function should be
- Not clear what the role of prediction should be
Types of RL Algorithms
Remember the objective of RL:
- Policy Gradient
- Directly differentiate the above objective
- Value-based
- Estimate value function or Q-function of the optimal policy (no explicit policy)
- Then use those functions to prove policy
- Actor-critic (A mix between policy gradient and value-based)
- Estimate value function or Q-function of the current policy, use it to improve policy
- Model-based RL
- Estimate the transition model, and then
- Use it for planning (no explicit policy)
- Use it to improve a policy
- Other variants
- Estimate the transition model, and then
Supervised Learning of RL
Model-Based RL
e.g.
- Dyna
- Guided Policy Search
Generate samples(run the policy) ⇒
Fit a model of ⇒
Then improve the policy(a few options)
Improving policy:
- Just use the model to plan (no policy)
- Trajectory optimization / optimal control (primarily in continuous spaces)
- Backprop to optimize over actions
- Discrete planning in discrete action spaces
- Monte Carlo tree search
- Trajectory optimization / optimal control (primarily in continuous spaces)
- Backprop gradients into the policy
- Requires some tricks to make it work
- Use the model to learn a separate value function or Q function
- Dynamic Programming
- Generate simulated experience for model-free learner
Value function based algorithms
e.g.
- Q-Learning, DQN
- Temporal Difference Learning
- Fitted Value Iteration
Generate samples(run the policy) ⇒
Fit a model of or ⇒
Then improve the policy(set )
Direct Policy Gradients
e.g.
- REINFORCE Natural Policy Gradient
- Trust Region Policy Optimization
Generate samples (run the policy) ⇒
Estimate the return
Improve the policy by
Actor-critic
e.g.
- Asynchronous Advantage Actor-Critic (A3C)
- Soft actor-critic (SAC)
Generate samples ⇒
Fit a model or ⇒
Improve the policy
Tradeoff between algorithms
Sample efficiency
“How many samples for a good policy?”
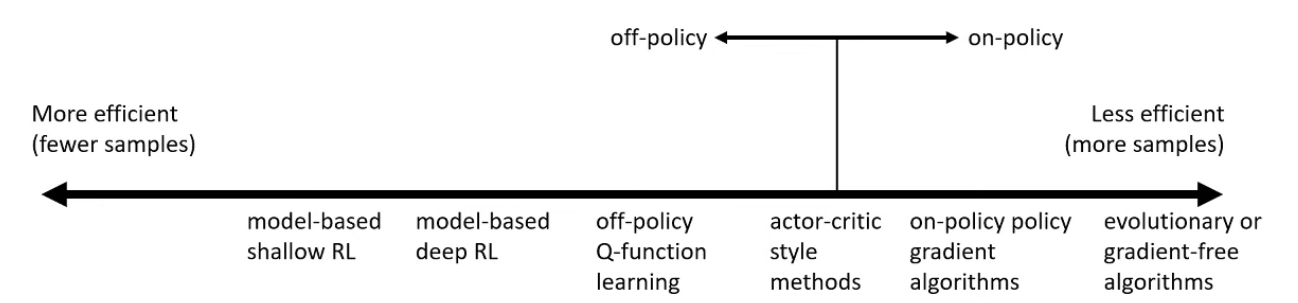
- Most important question: Is the algorithm off-policy?
- Off policy means being able to improve the policy without generating new samples from that policy
- On policy means we need to generate new samples even if the policy is changed a little bit
Stability & Ease of use
- Does our policy converge, and if it does, to what?
- Value function fitting:
- Fixed point iteration
- At best, minimizes error of fit (“Bellman error”)
- Not the same as expected reward
- At worst, doesn’t optimize anything
- Many popular DRL value fitting algorithms are not guaranteed to converge to anything in the nonlinear case
- Model-based RL
- Model is not optimized for expected reward
- Model minimizes error of fit
- This will converge
- No guarantee that better model = better policy
- Policy Gradient
- The only one that performs Gradient Descent / Ascent on the true objective
Different assumptions
- Stochastic or deterministic environments?
- Continuous or discrete (states and action)?
- Episodic(finite ) or infinite horizon?
- Different things are easy or hard in different settings
- Easier to represent the policy?
- Easier to represent the model?
Common Assumptions:
- Full observability
- Generally assumed by value function fitting methods
- Can be mitigated by adding recurrence
- Episodic Learning
- Often assumed by pure policy gradient methods
- Assumed by some model-based RL methods
- Although other methods not assumed, tend to work better under this assumption
- Continuity or smoothness
- Assumed by some continuous value function learning methods
- Often assumed by some model-based RL methods
Exploration
Offline RL (Batch RL / fully off-policy RL)
RL Theory
Variational Inference
No RL content in this chapter, but heavy links to RL algorithms
Control as an Inference Problem
Inverse Reinforcement Learning
Transfer Learning & Meta-Learning
Open Problems
Guest Lectures