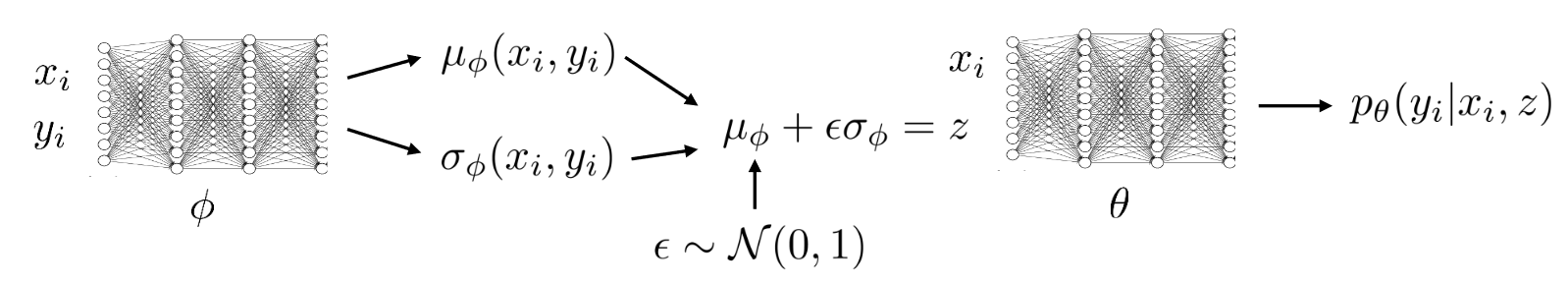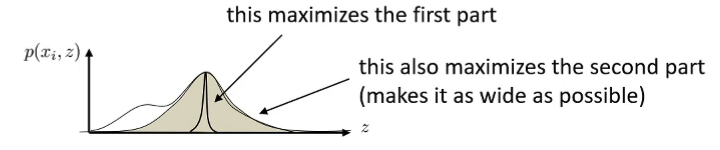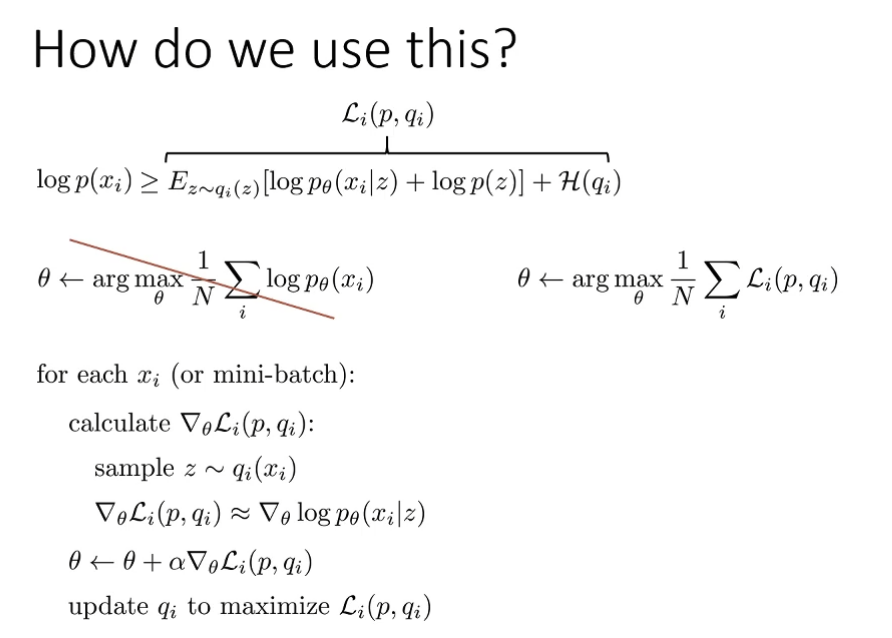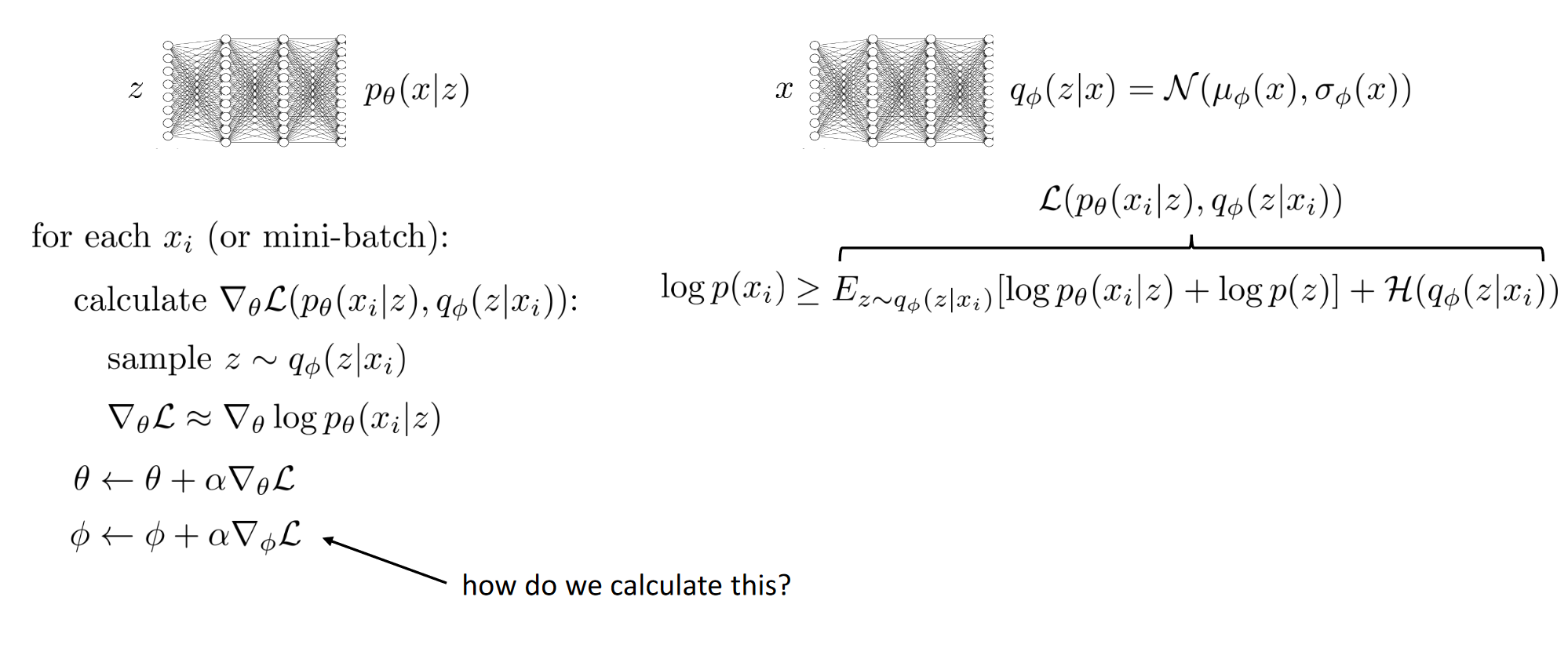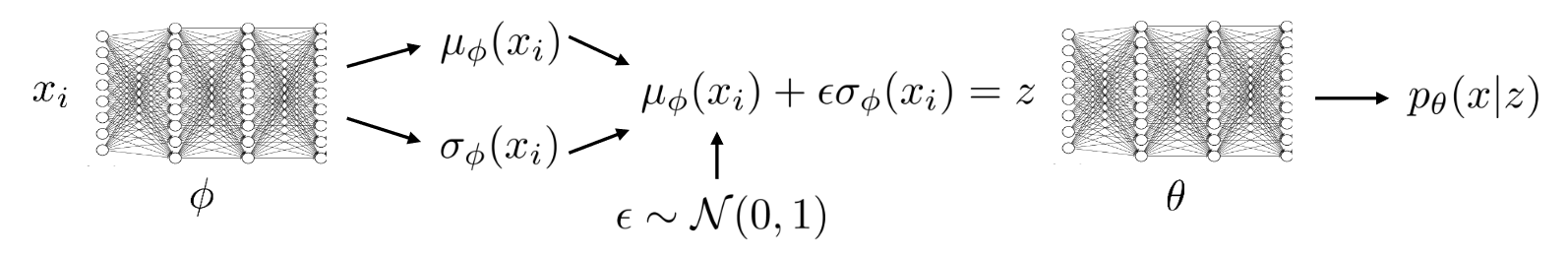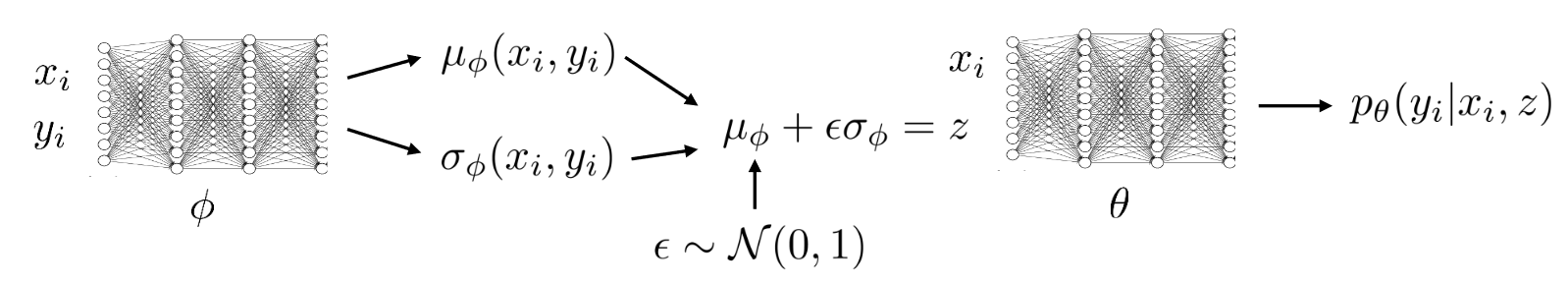Latent Variable Model
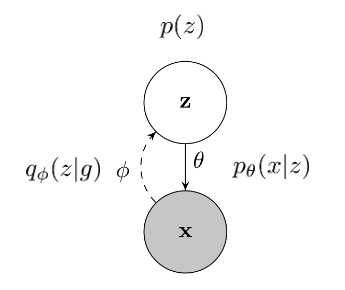 pθ(x∣z) ⇒ Latent Model (VAE) that transforms a proposed state z to x
pθ(x∣z) ⇒ Latent Model (VAE) that transforms a proposed state z to xWe have data points x, we want to model a distribution of x with the help of latent variable z.
How do we train latent variable models?
- Model pθ(x)
- Data: D={x1,x2,x3,…,xN}
- MLE fit: θ←argmaxθN1∑ilogpθ(xi)
- p(x)=∫p(x∣z)p(z)dz
- θ←argmaxθN1∑ilog(completely untractable∫pθ(xi∣z)p(z)dz)
Estimating the log-likelihood
🧙🏽♂️
Use Expected Log-likelihood
θ←θargmaxN1i∑Ez∼p(z∣xi)[logpθ(xi,z)] Intuition:
- Guess most likely z given xi, and pretend it is the right one
- But there are many possible values of z so use the distribution p(z∣xi)
- But how do we calculate p(z∣xi)?
- Approximate with qi(z)=N(μi,σi)
- Note that with each data point xi, they all have different qi
- With any qi(z), we can construct a lower bound on logp(xi)
- Maximize this bound (assume this bound is tight), we can push up on logp(xi)
logp(xi)=log∫zp(xi∣z)p(z)=log∫zp(xi∣z)p(z)qi(z)qi(z)=logEz∼qi(z)[qi(z)p(xi∣z)p(z)] Note:
Yensen’s Inequality (For concave function)
logE[y]≥E[logy] So
logp(xi)=logEz∼qi(z)[qi(z)p(xi∣z)p(z)]≥Ez∼qi(z)[logqi(z)p(xi∣z)p(z)]=Ez∼qi(z)[logp(xi∣z)+logp(z)]−Ez∼qi(z)[logqi(z)]=Ez∼qi(z)[logp(xi∣z)+logp(z)]+H(qi) 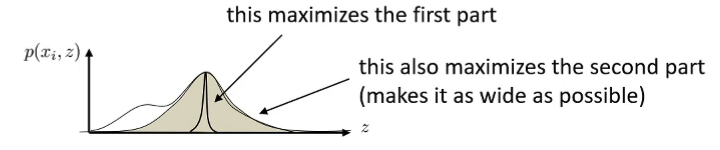
Note about entropy:
H(p)=−Ex∼p(x)[logp(x)]=−∫xp(x)logp(x)dx Intuitions:
- How random is the random variable?
- How large is the log probability in expectation under itself?
Also note about KL-Divergence:
DKL(q∣∣p)=Ex∼q(x)[logp(x)q(x)]=Ex∼q(x)[logq(x)]−Ex∼q(x)[logp(x)]=−Ex∼q(x)[logp(x)]−H(q) Intuitions:
- How different are two distributions?
- How small is the expected log probability of one distribution under another, minus entropy?
So the variational approximation
logp(xi)≥Ez∼qi(z)[logp(xi∣z)+logp(z)]+H(qi)Li(p,qi) So what makes a good qi(z)?
- qi(z) should approximate p(z∣xi)
- Compare in terms of KL-divergence DKL(qi(z)∣∣p(z∣x))
Why?
DKL(qi(z)∣∣p(z∣xi))=Ez∼qi(z)[logp(z∣xi)qi(z)]=Ez∼qi(z)[logp(xi,z)qi(z)p(xi)]=−Ez∼qi(z)[logp(xi∣z)]+logp(z)]+Ez∼qi(z)[logqi(z)]+Ez∼qi(z)[logp(xi)]=−Ez∼qi(z)[logp(xi∣z)]+logp(z)]−H(qi)+Ez∼qi(z)[logp(xi)]=−Li(p,qi)+logp(xi) Also:
logp(xi)=DKL(qi(xi)∣∣p(z∣xi))+Li(p,qi) In fact minimizing the KL-divergence has the effect of tightening then bound!
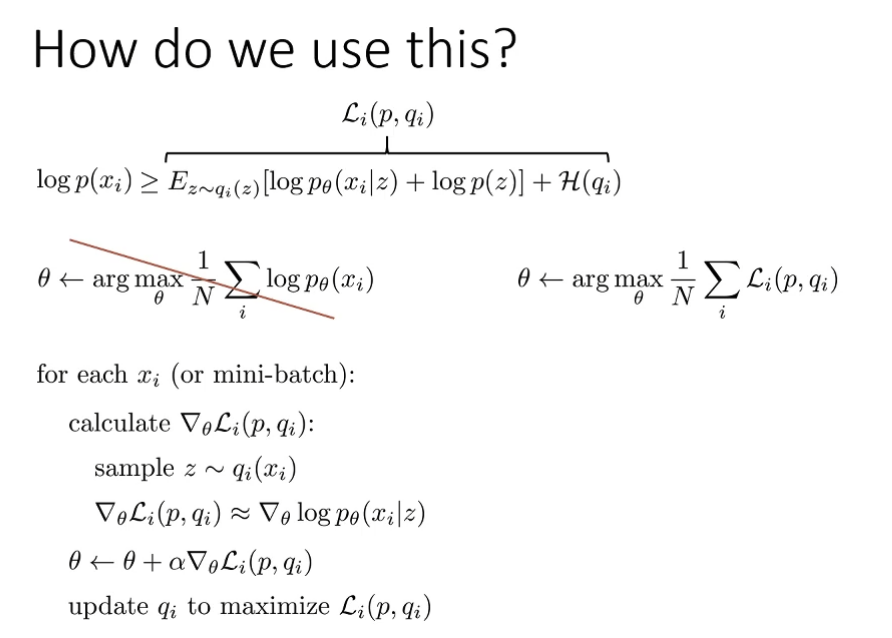
But how to improve qi?
- We can let qi=N(μi,σi) and use gradient ∇μiLi(p,qi) and ∇σiLi(p,qi)
- But too many parameters! We have ∣θ∣+(∣μi∣+∣σi∣)×N parameters
- Then can we use
- qi(z)=qϕ(z∣xi)≈p(z∣xi)?
- Amortized Variational Inference!
Amortized Variational Inference
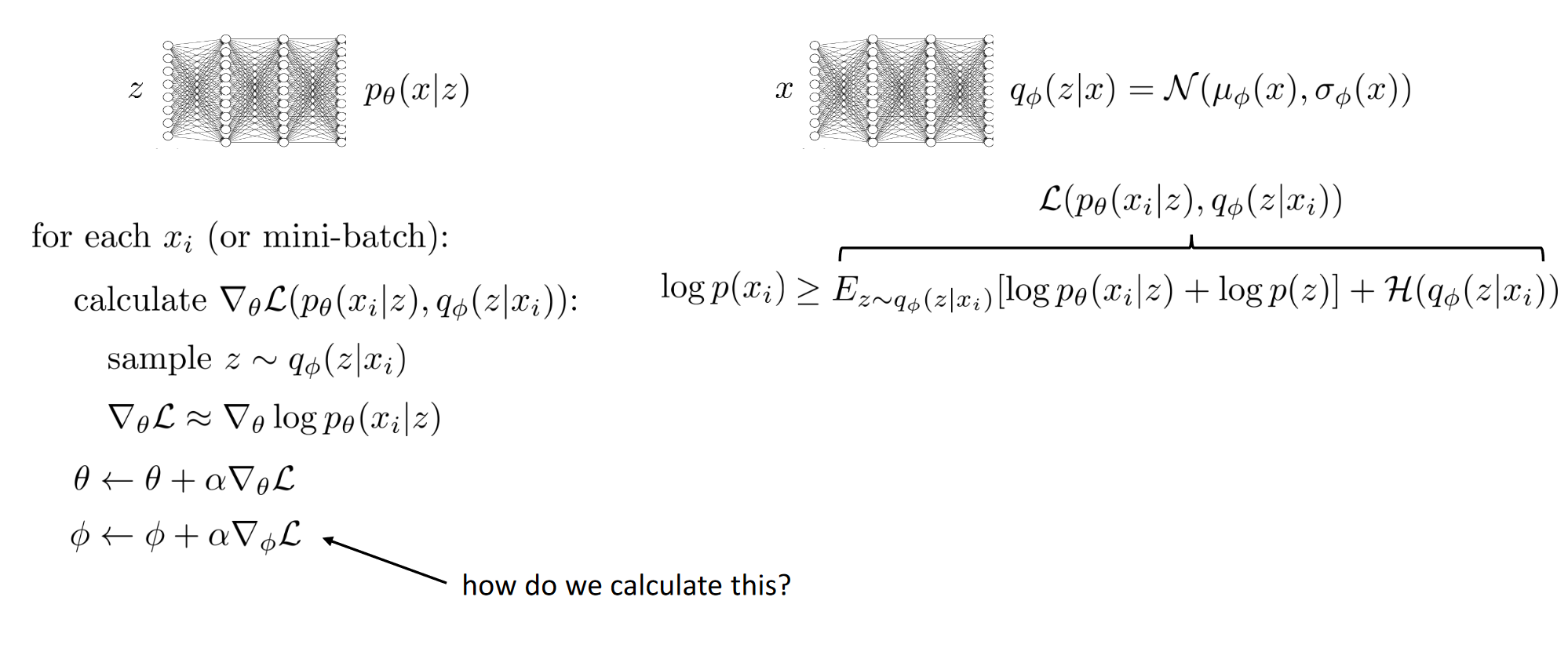
Li=J(ϕ)=Ez∼qϕ(z∣xi)[r(xi,z)]Ez∼qϕ(z∣xi)[logpθ(xi∣z)+logp(z)]+H(qϕ(z∣xi)) We can directly calculate the derivative for the entropy term but the first term J(ϕ) seems a bit problematic.
But this format looks a lot like policy gradient!
∇J(ϕ)≈M1j∑∇ϕlogqϕ(zj∣xi)r(xi,zj) What’s wrong with this gradient?
- Perfectly viable approach, but not best approach
- Tends to suffer from high variance
The reparameterization trick
⚠️
In RL we cannot use this trick because we cannot calculate gradient through the transition dynamics, but with variational inference we can
qϕ(z∣x)=N(μϕ(x),σϕ(x))z=μϕ(x)+ϵσϕ(x),ϵ∼N(0,1) This makes z an independent function of a random variable ϵ that is independent of ϕ
So now:
J(ϕ)=Ez∼qϕ(z∣xi)[r(xi,z)]=Eϵ∼N(0,1)[r(xi,μϕ(xi)+ϵσϕ(xi))] And now to estimate ∇ϕJ(ϕ)
- sample ϵ1,…,ϵM from N(0,1) (even a single sample works well)
- ϵ treated as a constant when computing gradient
- ∇ϕJ(ϕ)≈M1∑j∇ϕr(xi,μϕ(xi)+ϵjσϕ(xi))
This is useful because now we are using the derivative of the r function
Another Perspective of Li
Li=Ez∼qϕ(z∣xi)[logpθ(xi∣z)+logp(z)]+H(qϕ(z∣xi))=Ez∼qϕ(z∣xi)[logpθ(xi∣z)]+−DKL(qϕ(z∣xi)∣∣p(z))Ez∼qϕ(z∣xi)[logp(z)]+H(qϕ(z∣xi))=Ez∼qϕ(z∣xi)[logpθ(xi∣z)]−DKL(qϕ(z∣xi)∣∣p(z))=Eϵ∼N(0,1)[logpθ(xi∣μϕ(xi)+ϵσϕ(xi))]−DKL(qϕ(z∣xi)∣∣p(z))≈logpθ(xi∣μϕ(xi)+ϵσϕ(xi))−DKL(qϕ(z∣xi)∣∣p(z))
Reparameterization trick vs. Policy Gradient
- Policy Gradient
- Can handle both discrete and continuous latent variables
- High variance, requires multiple samples & small learning rates
- Reparameterization Trick
- Only continuous latent variables
- Simple to implement & Low variance
Example Models
VAE Variational Autoencoder
θ,ϕmaxN1i∑logpθ(xi∣μϕ(xi)+ϵσϕ(xi))−DKL(qϕ(z∣xi)∣∣p(z)) 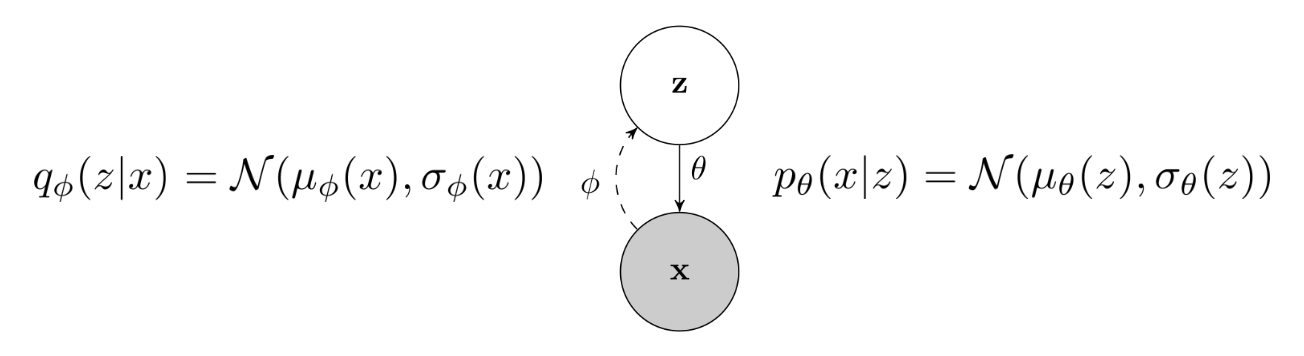
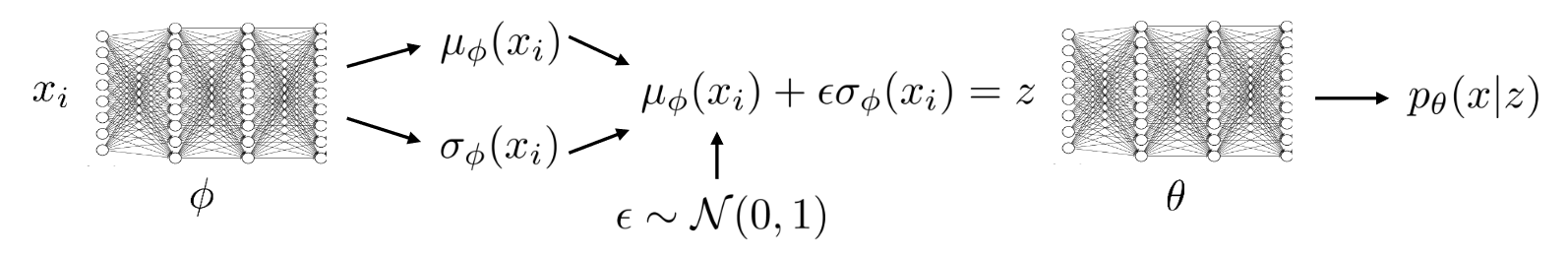
Conditional Models
Generates y given x,z
Li=Ez∼qϕ(z∣xi,yi)[logpθ(yi∣xi,z)+logp(z∣xi)]+H(qϕ(z∣xi,yi))